
The advantage of Latin hypercube in reducing noise reduces when the result depends on two or more uncertain quantities that have comparable effects on the result, with the noise increasing with the number of uncertain quantities performance of the Latin hypercube.
#Latin hypercube sampling equiprobable pdf
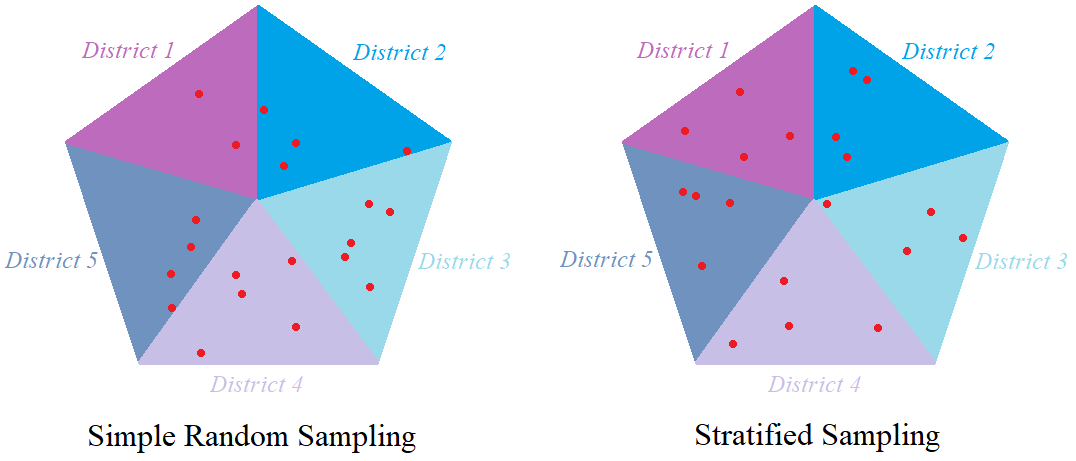
If you display the PDF of a variable that is defined as a single continuous distribution, or is a function of just one continuous uncertain variable, the distribution usually looks fairly smooth even with a small sample size (such as 20) with median Latin hypercube sampling - where simple Monte Carlo results looks quite noisy.

Median Latin hypercube, since it uses the median of each equiprobable interval is even more uniformly distributed than random Latin hypercube. The advantage of Latin hypercube methods is that they provide more uniform distributions of samples for each distribution than simple Monte Carlo sampling. However, since $ \log(n)^d $ is a very large number when d is even of moderate size, the guaranteed bound is not as useful as you might think. For a fixed d, Sobol's convergence rate at extremely large n approaches $ O(1/n) $, often seen as the holy grail of simulation. Monte Carlo sampling error converges as $ O(1/\sqrt) $ whereas Sobol converges as $ O(\log(n)^d / n) $, where d is the number of uncertain scalar quantities. Sobol sampling comes with a much stronger convergence guarantee than pure Monte Carlo sampling. It does this by applying Sobol sequences to each scalar quantity. Sobol samples in a way that coordinates across multiple dimensions, creating a more even sampling than Latin hypercube. Latin hypercube methods spread samples out uniformly for each scalar quantity separately, but since it samples from each quantity (dimension) independently, the coverage of the multidimensional space may not be very uniform. The Sobol Sampling method is a quasi-Monte Carlo method that attempts to spread sample points out more evenly in probability space across multiple dimensions than Monte Carlo or Latin hypercube methods. However, the samples are not totally independent because they are constrained to have one sample from each of the n intervals. With random Latin hypercube sampling, each sample is a true random sample from the distribution, as in simple Monte Carlo. The random Latin hypercube method is similar to the median Latin hypercube method except that, instead of using the median of each of the m equiprobable intervals, it samples at random from each interval. These points are then randomly shuffled so that they are no longer in ascending order, to avoid nonrandom correlations among different quantities. The sample points are the medians of the m intervals, that is, the fractiles: Median Latin hypercube sampling is the default method: It divides each uncertain quantity X into m equiprobable intervals, where m is the sample size. You can therefore use standard statistical methods to estimate the accuracy of statistics, such as the estimated mean or fractile (percentile) of a distribution, as described in Selecting the Sample Size.
With the simple Monte Carlo method, each value of every random variable X in the model, including those computed from other random quantities, is a sample of m independent random values from the true probability distribution for X. It then uses the inverse of the cumulative probability distribution to generate the corresponding values of X, Analytica generates m uniform random values, u i, for i = 1, 2.m, between 0 and 1, using the specified random number method (see below). In this method, each of the m sample points for each uncertainty quantity, X, is generated at random from X with probability proportional to the probability density (or probability mass for discrete quantities) for X. The most widely used sampling method is known as Monte Carlo, named after the randomness in games of chance, such as at the famous casino in Monte Carlo.


 0 kommentar(er)
0 kommentar(er)
